Bogosort

配列の要素をランダムに並び替えて, 運良くソートできていればソート完了というソートアルゴリズム. 配列のサイズが $N$ で, 要素がすべて異なるとしたとき, 平均計算時間は $O(N \cdot N!)$ .

要素の交換回数の期待値は $(N - 1) \cdot N!$ となる *1.

Bozosort

Bogosort の変種で, すべて並び替える代わりに, ランダムに 2 つの要素を選んで交換する. 平均計算時間は $O(N!)$ , 要素の交換回数の期待値は $\sim N!$ らしい *2 ので, Bogosort よりも効率が良い.

改悪

今回は Bozosort の交換部分を少し変更して, 効率を悪化させることを考える. 配列のサイズは $N$ で, 要素はすべて異なり, 連番の自然数 $1, 2, \cdots, N$ であるとする.

Bozosort の要素の交換は完全にランダムに行っているが, ここでは要素をソートされにくくなるように選ぶように変更する. まず, 配列に対してコストを,

${ \begin{align*} E = \epsilon \sum_{i = 1}^{N - 1} \left(\left|n_{i + 1} - n_i\right| - 1\right) \end{align*} }$

と定義する. $\epsilon$ は適当な係数で, 今は $\epsilon = -1$ としておく, すなわち, 隣り合う要素の差が大きい (ソートされていない) ほどコストが下がる ようにする.

次に, 適当なインデックス $i, j$ を選んだとき, 要素を交換する確率 $p$ を,

${ \begin{align*} p = \min\left\{1, \exp(-\beta \Delta E_{ij})\right\} \end{align*} }$

とする. ただし, $\beta \geq 0$ は適当なパラメータ, $\Delta E_{ij}$ は交換の前後のコストの変化で, 交換の後にコストが下がる ( $\Delta E_{ij} \lt 0$ ) なら常に交換, コストが上がる ( $\Delta E_{ij} \gt 0$ ) なら一定確率で交換しないようにする. $\beta = 0$ の場合は常に交換するため, Bozosort と同じである. ここの確率の選び方はコストが上がる時に交換をしたがらないようにすれば割と適当で良い気がするが, ソートが不可能とならないように, コストが上がる場合でも一定確率で許容するように注意する.

このようにして,

適当なインデックス $i, j$ を選ぶ
要素の交換を試行する
ソートできたら終了, できていなければ 1 に戻る

という Bozosort の改良 (改悪) ソートアルゴリズムができた (特に良い名前も思いつかないのでとりあえず Bakasort と呼ぶことにする).

実験

実際に Bogosort, Bozosort, Bakasort についてソートを行い, 平均交換回数を (Bogosort については平均並び替え回数を, Bakasort については平均試行回数も) 調べた (Bogosort および Bakasort ( $\epsilon = -1$ ) については 100 回, それ以外は 1000 回の平均).

f:id:susisu:20160507233320p:plain

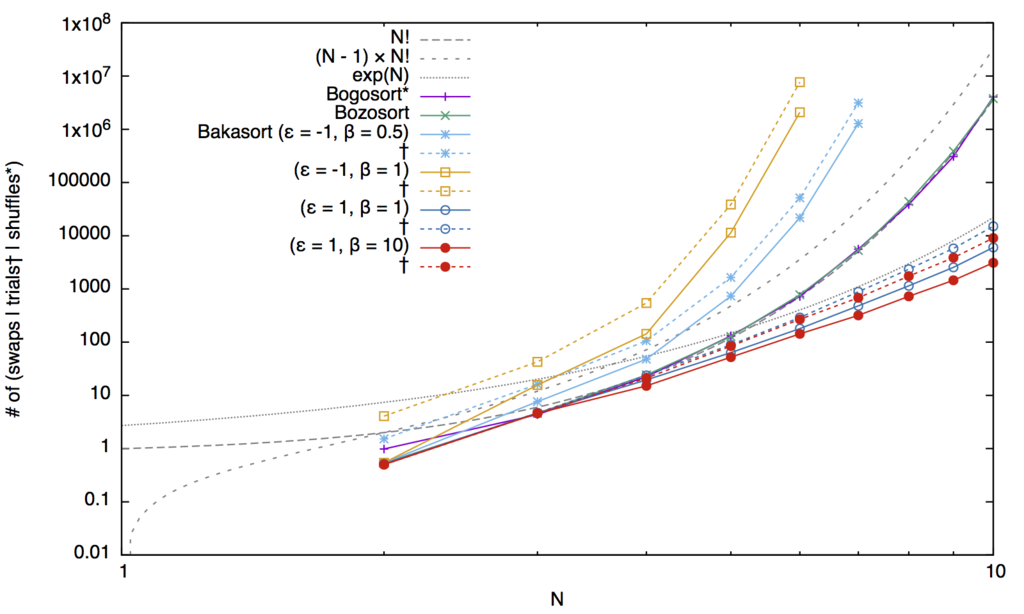
これを見ると, Bakasort は Bozosort ( $\sim N!$ ) だけでなく Bogosort ( $(N - 1) \cdot N!$ ) に比べても効率が悪くなっていることがわかる (具体的にどの程度悪いかは数学弱者なのでよくわからなかった). 今回は $\beta = 0.5, 1$ の場合について調べたが, $\beta$ を大きくすればいくらでも効率は悪くなるはずである (もちろん, あるところでコンピューターの計算上 $p = 0$ になってしまうのでソートが不可能になるのだが).

おまけとして, Bakasort の $\epsilon = 1$ とした場合についても調べた. こちらはソートされるような交換を好むので, 効率は Bozosort よりも良くなり, この範囲で見る限り, およそ指数関数程度の増加になっているようだ (うっかり逆順にソートされてしまうとかなり効率が悪くなる気がするけれど大丈夫なんだろうか).